一丶反向传播算法
1.反向传播算法原理
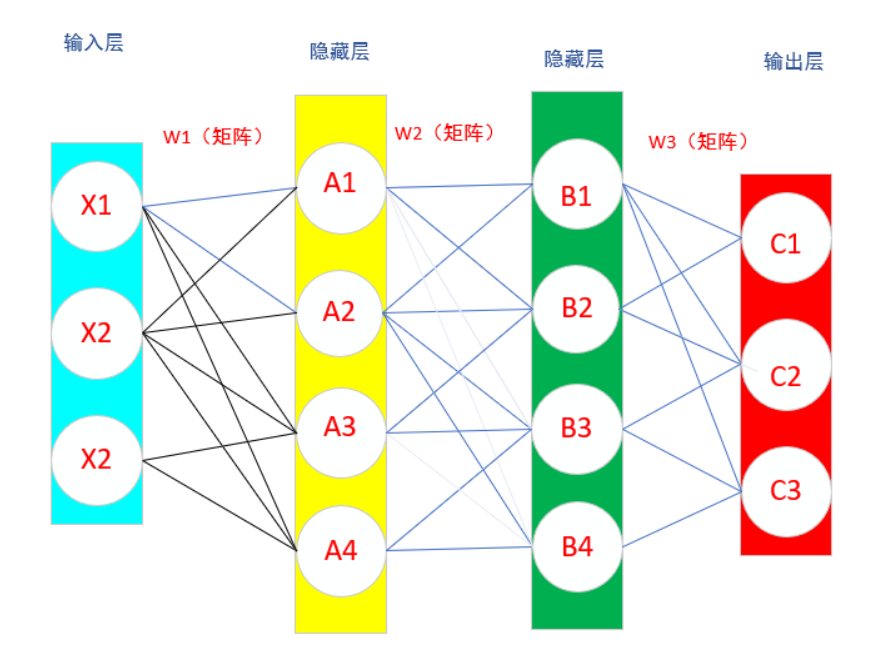
要搞懂反向传播算法，首先弄清目的是为了什么，最终就是求误差函数对权重的导数，求到了可以干什么呢,看下图，
这个公式是不是很眼熟，就是逻辑回归的权重更新公式，只不过变成二维，例如：w12表示上图X1-A2权重，求出误差函数对每个权重导数，设置一个学习率，通过不断更新权重，使得误差函数越来越小，训练出一个好的模型。
那要怎么求误差函数对权重导数呢，其实就是链式求导，已知有输入X,权重（随机赋予），原始输出，激活函数（sigmoid），误差函数。
有了这些值可以求出上图各个神经元的输出（正向传播）：举个栗子，上图
对于A1神经元：
这只是第一层隐藏层 ,到第二层，输出层，就是一层套着一层，误差函数就是原始输出跟预测输出的差值，所以当我们要求误差函数对权重导数:例如对W11,
其中右边第一项还要继续拆分，这里不展开了。反正每一项大概都是这样求。 自此，基本完毕！
下面讲个例子，我相信大家应该懂了，不对是肯定懂了 。
2. 反向传播算法实例
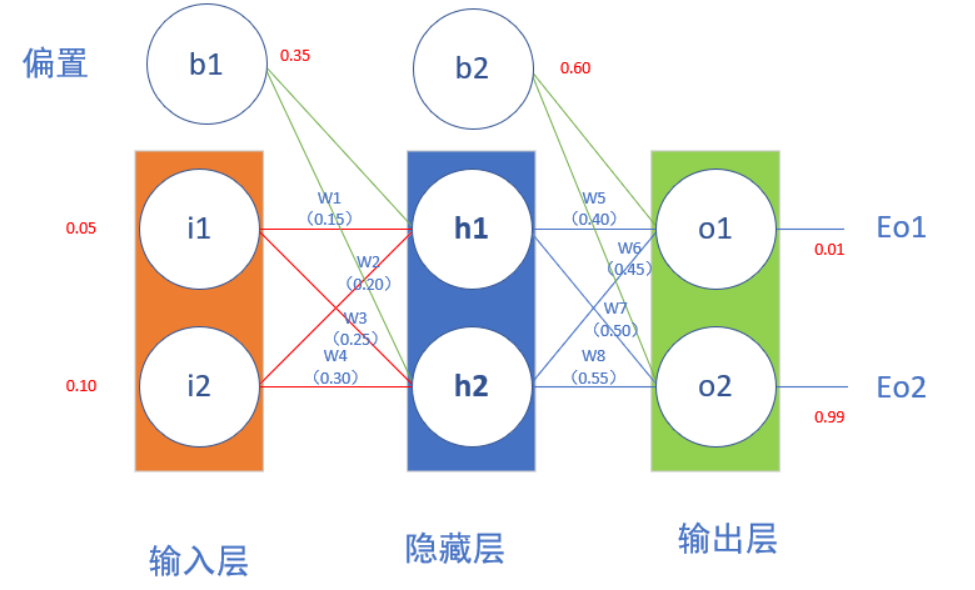
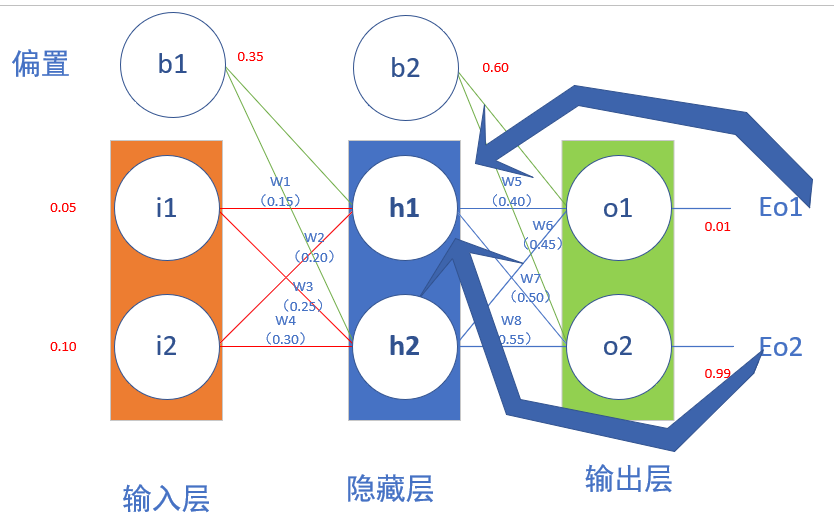
假设存在以下神经网络，给出初始化权重和偏置量，激活函数为sigmoid
2.1先算前向传播
- 先计算h1，h2：
同理可得： 
紧接着算下一层的o1，o2：
同理可得：
2. 计算误差
同理可得：
2.2 计算反向传播
输出层：对于w5，想知道其改变对总误差有多少影响，于是得
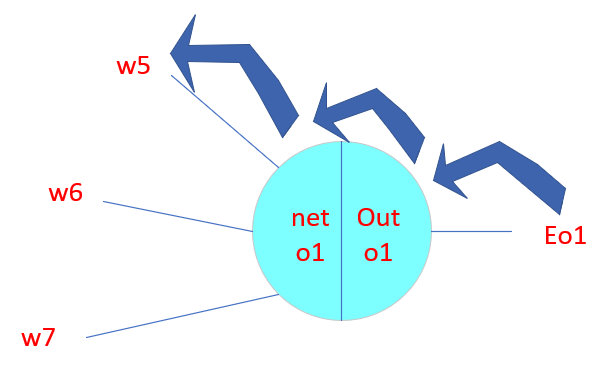
查看上图，其实反向传播就是链式求导，E可以理解为误差函数，就是先随机赋值权重，然后进行正向传播，得到各个神经元的输出，然后反向求导对权重，带入正向传播求出的数值，得到误差函数对各个权重的导数，设置学习率，利用梯度下降不断更新权重，最后得到合适的权重。与逻辑回归算法类似。
- 如何求上述误差函数对w5求导公式，一步一步来：
2.
3.
由此可得：
为了减少误差，然后从当前的权重减去这个值（可选择乘以一个学习率，比如设置为0.5），得：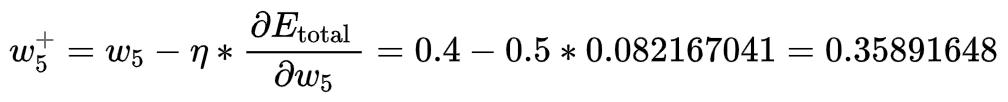
又是熟悉的配方，按照上述步骤，可求其他权重。
- 接下来求误差函数对w1的导数
要想对w1求导，就需要对h1求导，而h1分别有w5，w7与o1，o2相连，所以求导公式稍变化
这个与前面相差不大，合起来无非是变成两项，分别求出各项（有点想吐放松一下）
1
2.
3.综合可得，第二个公式按照上面步骤同理可得：
合并：
因为sigmoid函数求导公式为g(z)' = g(z)*(1-g(z))
全部合并：
终于到最后一步了，不容易：
同理：
2.3 总结
至此，算完了一轮更新的权重（w1 - w8），将他们重新带入神经网络，输出将会和原始输出差距减小，经过不停地迭代，最终误差函数会越来越小。
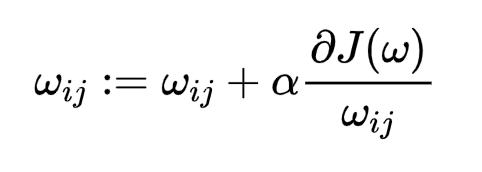
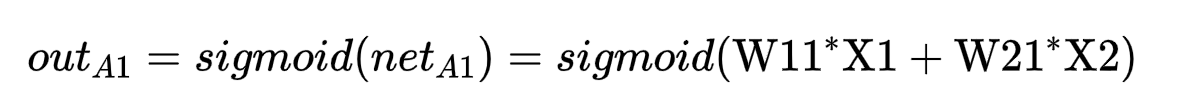
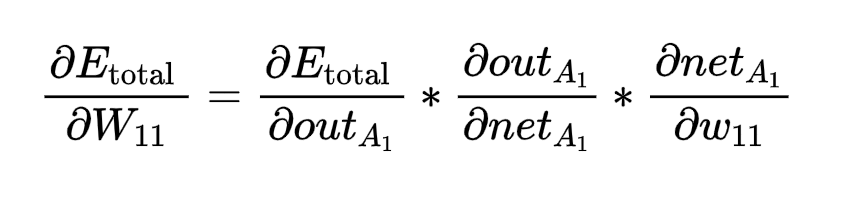
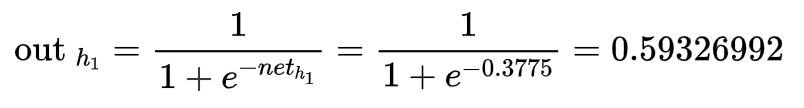
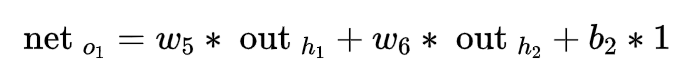
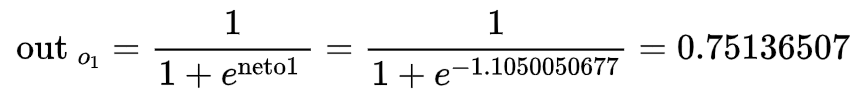
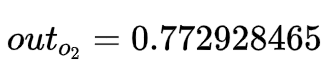
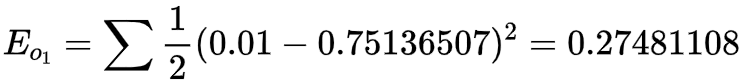
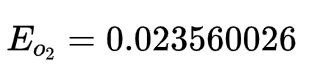
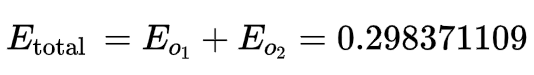
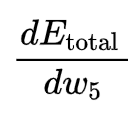
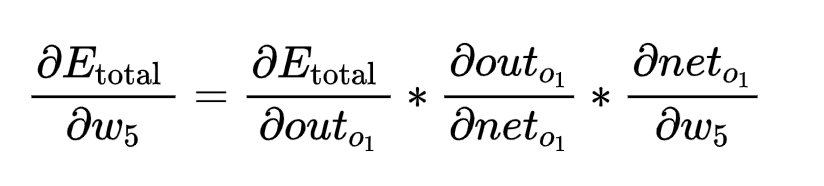
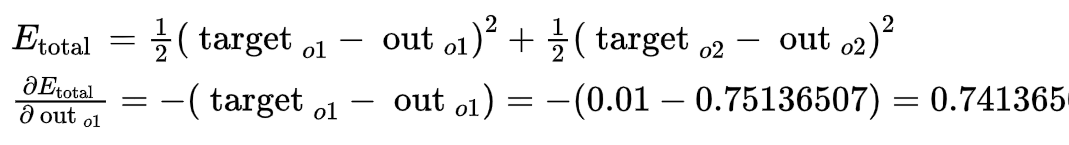
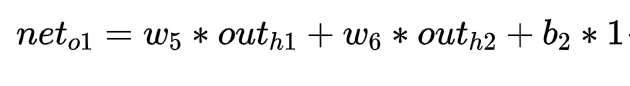
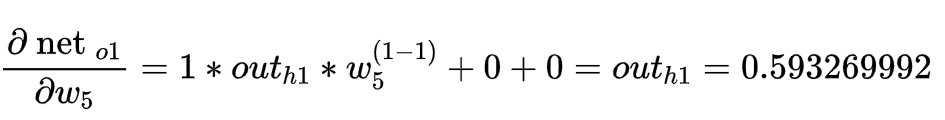
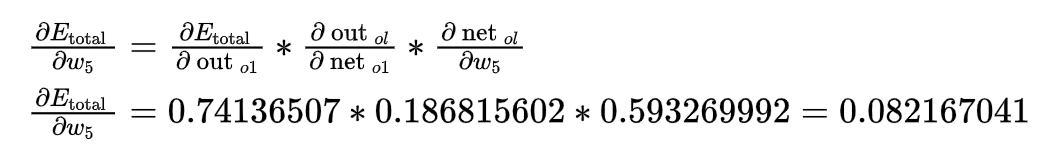
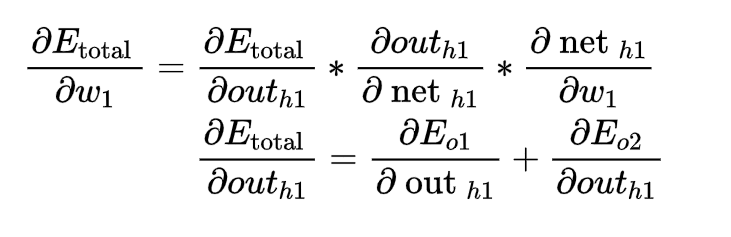
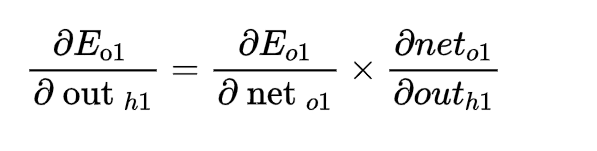
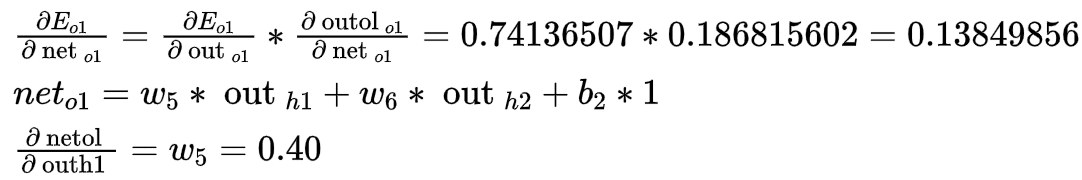
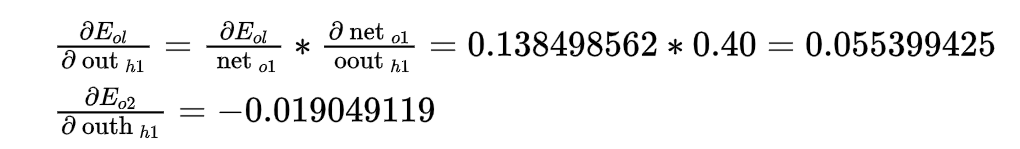
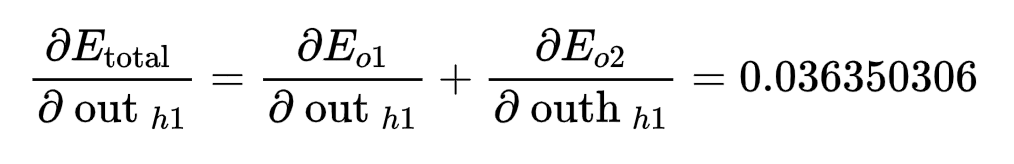
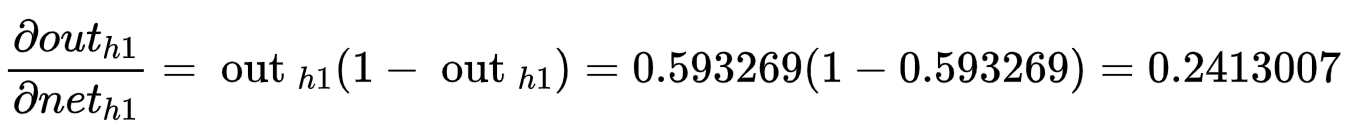
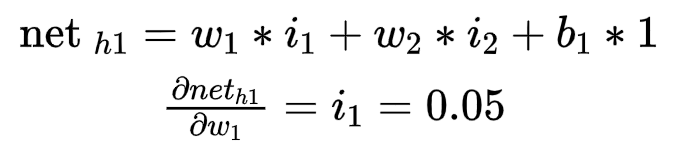
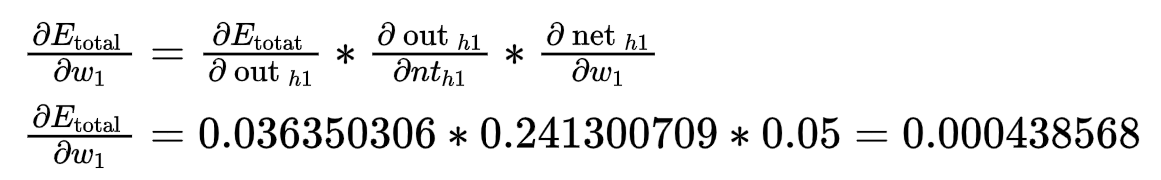
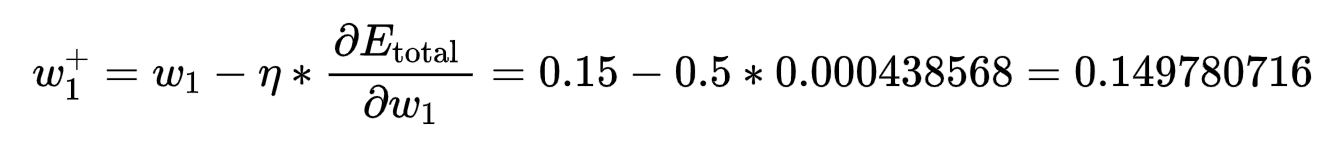
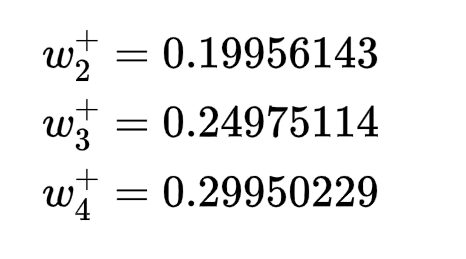
评论